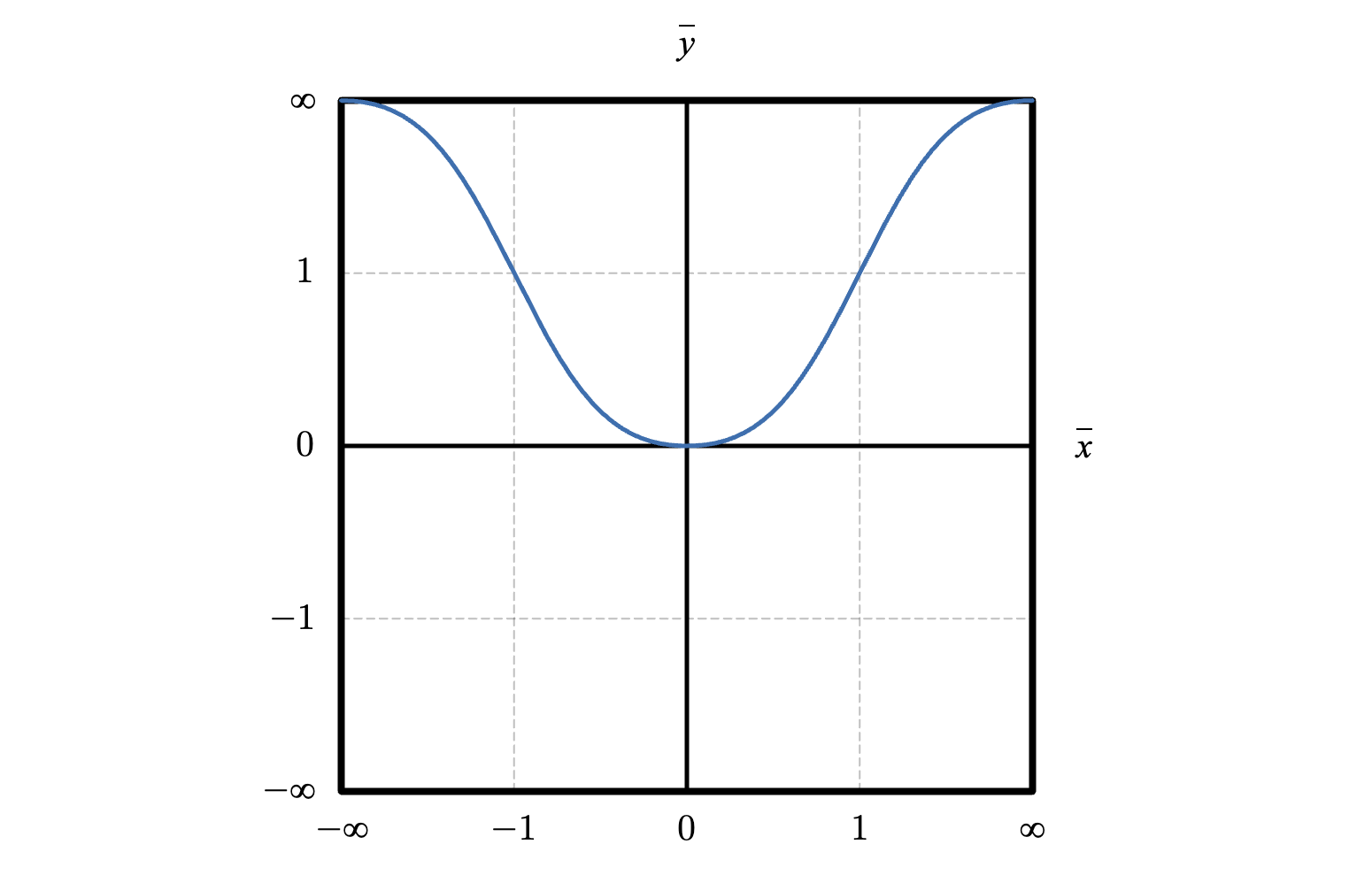
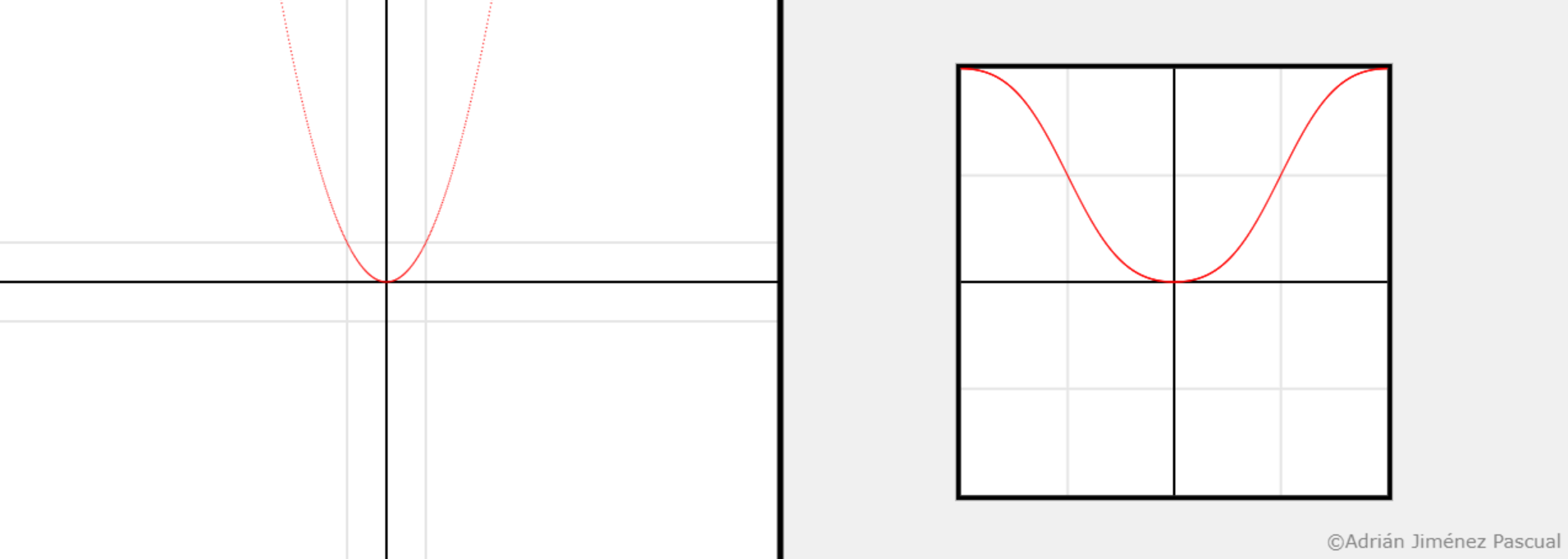
• Parabola $x^2$ on the left and its fenced representation on the right.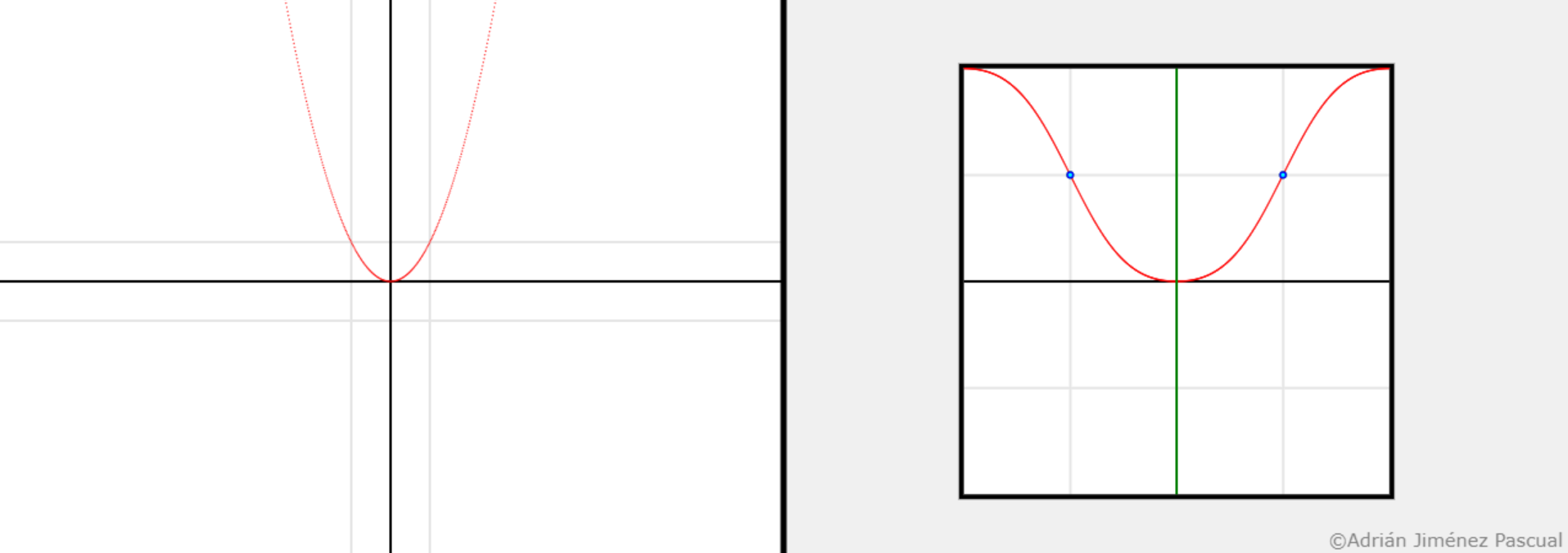

      • $$\tau : \mathbb{R} \rightarrow (-1, 1)\qquad\qquad \tau(x)=\frac{x}{1+\mid x \mid}$$

      • The parabola $x^2$ has one axial symmetry and two branch symmetrie about a point.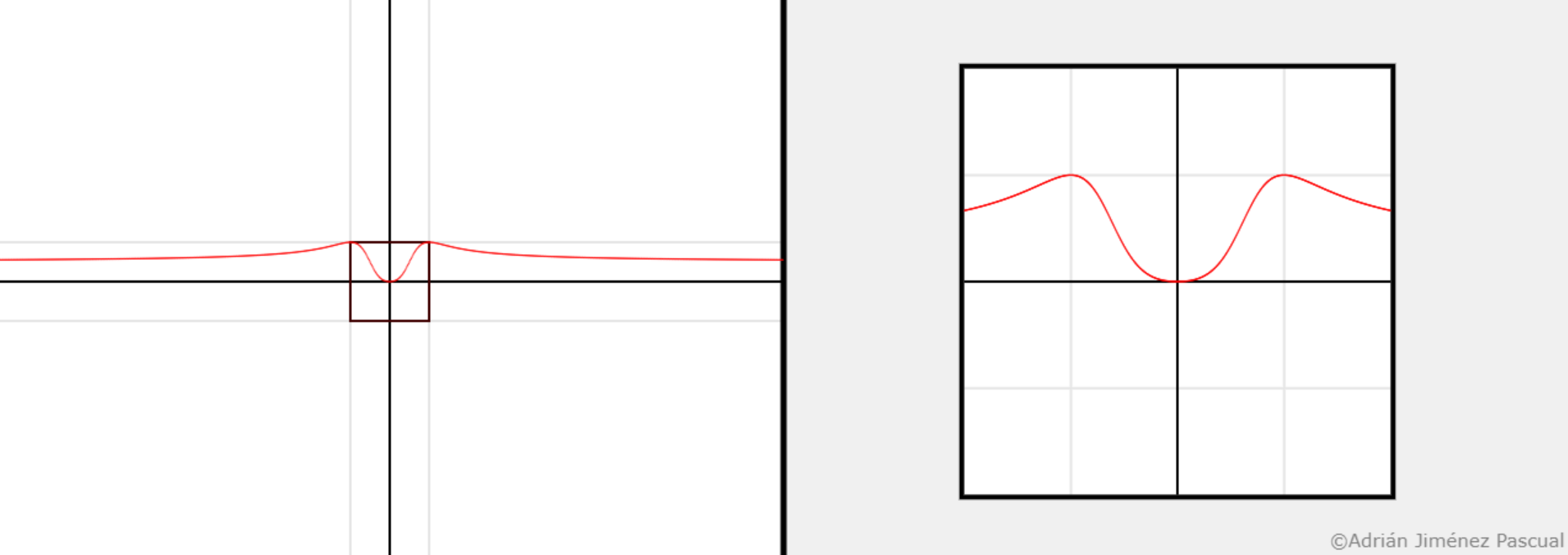

      • Left: Fenced representation of the parabola $x^2$ interpreted as the input function.
      Right: Fenced representation of it.